Quantum Embeddings for Anomaly Detection: A New Lens on Data Representation

- Detecting rare or unusual patterns requires working with large, complex data.
- Traditional machine learning loses accuracy when data has many features but few examples.
- Quantum machine learning can uncover patterns classical methods miss, but is limited by low qubit counts to low-dimensional datasets.
- Haiqu’s new quantum encoding solution packs hundreds of features into just a few qubits and scales efficiently, removing a major barrier to real-world data processing on a quantum computer.
Anomalies are the world’s early warning systems. They appear as subtle ripples before an earthquake, a sudden deviation in a patient’s vital signs, or a single fraudulent transaction hidden among millions of legitimate ones. Detecting such rare events is essential for safety, trust, and reliability in modern data-driven systems. Still, it remains one of the hardest problems in machine learning.
The reason lies in their rarity. By definition, anomalies are statistical outliers, making up only a fraction of a dataset. Classical models must learn to recognize these events despite being trained predominantly on normal examples. And in practice, the data itself compounds the difficulty. Hundreds of correlated features, nonlinear dependencies, and limited examples make it hard for algorithms to find meaningful structure.
Classical approaches like decision trees, logistic regression, and deep neural networks have achieved remarkable progress, but even the best of them eventually plateau. Particularly at high dimensionality and low sample size, they begin to lose their footing. This is where quantum computing, with its fundamentally different way of representing and processing information, may offer a new path forward.
Jay Gambetta, Director of IBM Research
Where Classical Representations Fall Short
Machine learning is dependent upon how we represent data. The features describing the data determine what a model can perceive, and, as a result, what it can learn. The goal of kernel methods and, more broadly, of representation learning is to construct new data features, often by embedding in larger spaces, which “expose” the inherent patterns in the data [1]. This allows downstream machine learning models to achieve better performance in e.g. classification tasks. In most real-world data, however, the relations between these features are nonlinear and strongly correlated, which poses a major challenge to classical methods.
Quantum systems, by contrast, naturally take advantage of superposition and entanglement to process unstructured feature vectors [2]. This allows both to embed data in an exponentially larger space of multi-qubit states and to reveal its structure through the use of quantum dynamics, enabling efficient classification. In other words, mapping classical data into this space effectively expands the representational canvas and allows the discovery of patterns that classical embeddings may flatten or miss entirely.
This concept is central to quantum machine learning. Through quantum embeddings, data is transformed into quantum states, and similarities between samples are evaluated via quantum kernels, comparable to kernel methods in classical machine learning but powered by the physics of interference. Even when run in simulation, these quantum representations reveal how computation in Hilbert space can enrich classical preprocessing [2].
Prof. Oleksandr Kyriienko, Professor and Chair in Quantum Technologies at the University of Sheffield.
Encoding Data of Previously Impossible Size
The first step to constructing a quantum embedding is to encode the original data in a quantum state, which is then transformed using e.g. quantum dynamics. While many existing studies rely on angular encodings, such methods quickly reach their limits as the number of qubits required grows linearly with the number of data features [3, 4]. Most near-term quantum devices have fewer than 150 qubits, yet anomaly-detection and other real-life datasets can easily contain hundreds or thousands of features. This creates a dimensionality gap that makes naïve quantum feature maps impractical.
Near-term quantum devices have fewer than 150 qubits, making naïve feature encodings impractical for real-world datasets with hundreds or thousands of features.
To address this challenge, we developed a novel data encoding method, which allows us to encode polynomially more features with the same number of qubits. Moreover, our method awards control over the complexity of the resulting quantum state and of the quantum circuit creating it. This permits adjusting the embedding to both the number of features in the data, as well as to the parameters of the QPU. Our dataset contained 506 classical features which we mapped onto 128 qubits, but the same QPU could be used to encode an order of magnitude larger feature numbers with our technique.
We develop an encoding solution that allows an order of magnitude more features to be loaded on a QPU.
The resulting embeddings can be used as feature transformations in any machine-learning pipeline, feeding quantum-enriched data into classical models. This hybrid structure of classical models trained on quantum-preprocessed data forms the foundation of our experiment.
Dr. Kristin Milchanowski, Chief AI and Data Officer, BMO
A Head-to-Head Comparison
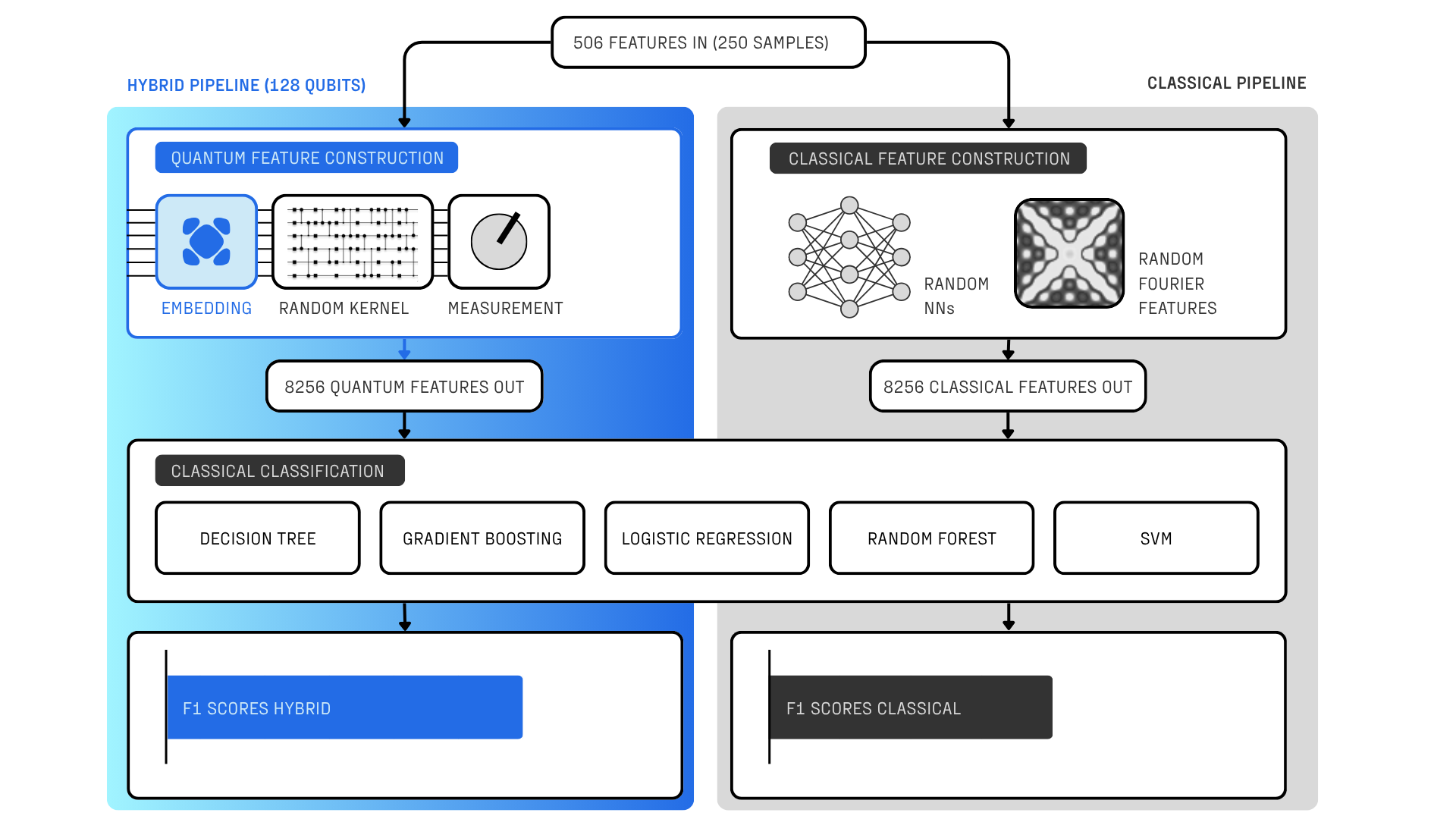
To test the performance of our quantum embeddings against their classical counterparts task we designed an experiment with two parallel pipelines: a hybrid one (quantum+classical), and a fully classical one, as shown in Figure 1. The inputs to both are constructed from the Multivariate Time Series Anomaly benchmark used to evaluate the detection of rare events in temporal data. Our dataset consists of a smaller and balanced subset of 250 samples of coarse-grained time-series, where time-points within time windows in the original data have been merged together to form high-dimensional vectors of 506 features.
Fairness of comparison was central to our evaluation of the potential of quantum embeddings. In both pipelines, data is embedded into an enlarged space. In the quantum setting, we apply our novel data encoding, evolve the system under a parameterized quantum circuit implementing Heisenberg dynamics with randomly chosen parameters, and measure the resulting state to obtain new classical features. This is a form of projected quantum kernel (PQK) [3, 4]. In the classical pipeline, we tested two forms of embeddings with the same number of parameters as the quantum model: neural networks with random parameters, and random Fourier features. These embeddings produced new classical features of the same dimensionality as those generated by the quantum feature map.
Both the quantum-processed and classically-generated features were then input into the same families of classical classifiers, such as random forests and logistic regression. The hyperparameters of each classifier were independently optimized to ensure the best possible performance within each pipeline. We employed an 80/20 train–test split and evaluated performance using the F1 score, which balances precision and recall for imbalanced classification tasks.
Results: Quantum-Enhanced Preprocessing Works
In ideal simulations, our projected quantum kernel (PQK) achieved an F1 score of 0.98, outperforming classical baselines of around 0.90–0.93. Even on real quantum hardware, in this case an IBM Quantum Heron processor, where noise and gate infidelity introduce imperfections, the model retained an impressive 0.96 F1, showing that the method is both effective and robust under realistic device conditions.

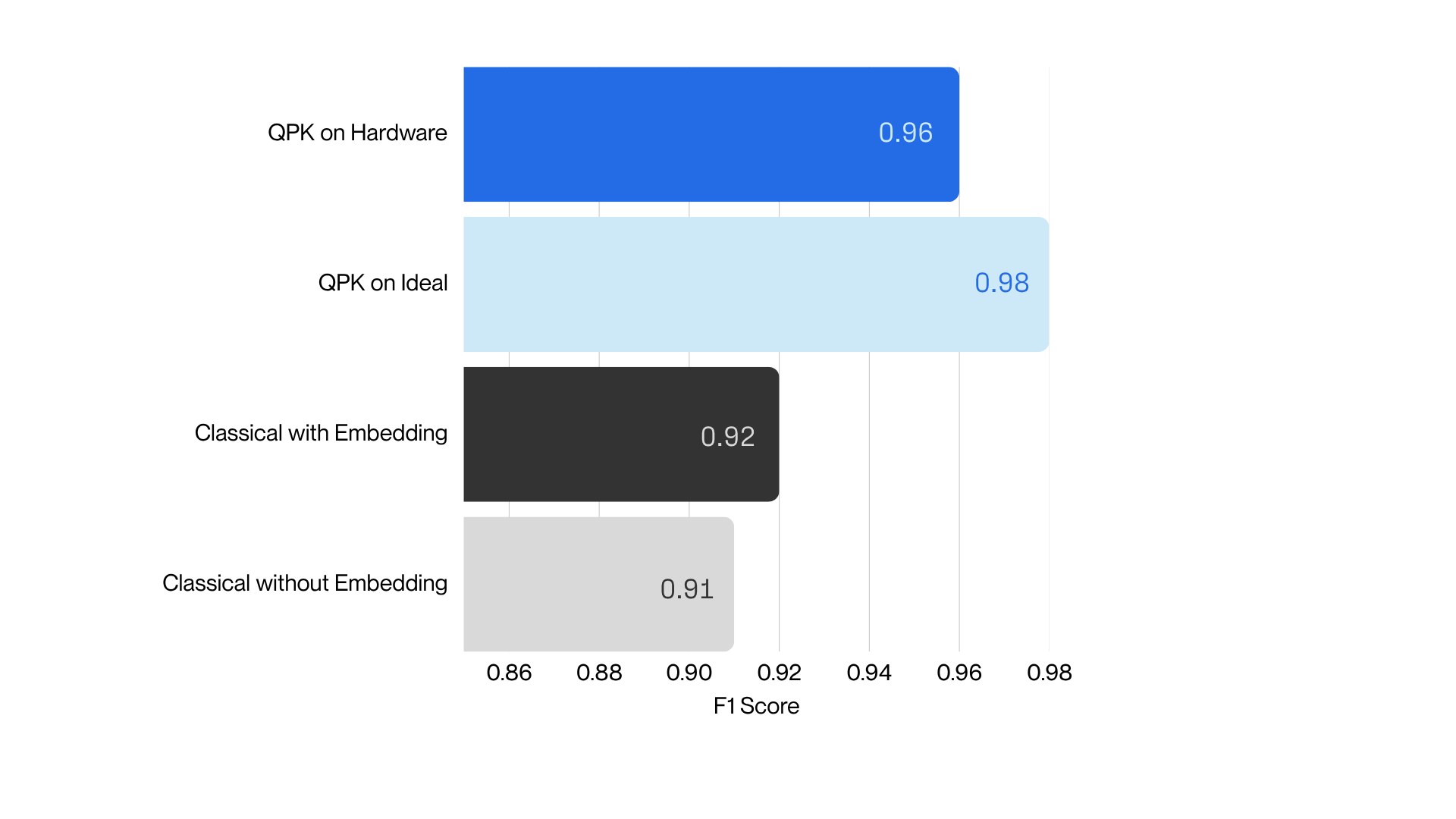
Figure 2. Left: The F1 score of different classical classifiers using either the classical (black) or the quantum (blue) features obtained on the IBM Quantum Heron processor. For most classifiers the quantum features provide better performance. Right: A more detailed comparison for the Logistic Regression Classifier. The classifier with original input data achieves an F1 score of 0.91, while the random classical embeddings essentially do not improve the score (0.92). In contrast, using the random quantum embedding a score of 0.98 is obtained when simulated without noise, and 0.96 when executed on the real noisy quantum processor.
The largest relative improvements appeared in tree-based models such as Decision Trees and Random Forests, which benefited most from the richer feature representations. Across the board, these results suggest that quantum embeddings can serve as a general-purpose preprocessing layer, improving performance without changing model complexity or parameter count. In other words, quantum systems need not replace classical models, but augment them.
A Glimpse of the Future
The importance of our findings is threefold:
- First, it shows that quantum-enhanced features can achieve superior performance over classical embeddings in complex data.
- Second, that extremely high-dimensional data can be embedded using our methods on existing QPUs.
- Third, we show that this superior performance is present both in idealized simulation that validates the pipeline, and on real noisy quantum hardware.
Taken together, the results provide an empirical signal that quantum advantage with QML may be possible to achieve in full-fledged industrial deployment to complex high-dimensional problems, and that investigating efficient quantum data embeddings on real datasets is a promising path towards realizing that advantage.
This holds even without training the embedding weights, which should further improve the features, and thus the final performance.
With increasing problem size (and thus qubit numbers and circuit depth) classical simulations will become completely infeasible, but already at smaller scales it may become advantageous to use the QPU at least for the inference from a trained kernel.
Thus, a hybrid QML pipeline which achieves superior performance in a complete end-to-end industrial deployment will likely involve
- a classical pre-training step of the quantum embedding using large scale simulation,
- followed by an optional fine-tuning step on a QPU,
- and finally, an inference step performed at test time on a QPU.
This hybrid workflow could extend beyond anomaly detection into fields like cybersecurity, financial modeling, predictive maintenance, and health diagnostics, all domains where interpretability and early warning signals matter most.
A Call To Explore
Our anomaly-detection study provides early evidence that quantum-enhanced preprocessing is practically meaningful even on today’s noisy hardware. Out study demonstrates how hybrid pipelines can achieve measurable gains without increasing model complexity, parameter count, or data requirements.
We are now preparing to share interactive notebooks that allow verified beta users to reproduce this experiment using Haiqu’s embedding technology. These tools will enable researchers and developers to explore quantum preprocessing within their own domains, from time-series analysis to computer vision, and benchmark their results against classical baselines.
We invite the community to join this exploration: replicate, challenge, and build upon our results. Each successful reproduction strengthens the case for a future where quantum and classical computation work hand in hand, and where models understand data more deeply.
References:
[1] Shawe-Taylor, John, and Nello Cristianini. Kernel methods for pattern analysis. Cambridge university press, 2004.
[2] Schuld, Maria, and Francesco Petruccione. Machine learning with quantum computers. Vol. 676. Berlin: Springer, 2021.
[3] Schnabel, J., and M. Roth. "Quantum kernel methods under scrutiny: A benchmarking study (2024)." arXiv preprint arXiv:2409.04406.
[4] D'Amore, Francesco, Luca Mariani, Carlo Mastroianni, Francesco Plastina, Luca Salatino, Jacopo Settino, and Andrea Vinci. "Assessing Projected Quantum Kernels for the Classification of IoT Data." arXiv preprint arXiv:2505.14593 (2025).
